Zeitreisen mit persistenten Datenstrukturen
Zeitreisen mit persistenten Datenstrukturen
Wir schreiben das Jahr 2025. Längst haben soziale Plattformen im Internet uns vollständig von der Notwendigkeit eines guten Gedächtnisses befreit. Ein Großteil der Kommunikation ist für die Ewigkeit auf Servern gespeichert und kann jederzeit abgerufen werden.
In einem Anflug von Nostalgie erinnern wir uns an die guten alten Zeiten um das Jahr 2013 und fragen uns, warum unsere Lieblingsplattform es uns nicht erlaubt abzufragen, wer denn damals unsere „Freunde“ und Freundesfreunde waren.
Sicherlich nicht, weil das nicht möglich ist. Virtuelle „Zeitreisen“ wie diese sind durchaus möglich und in vielen Fällen sogar effizient realisierbar. Am Beispiel eines Freundschaftsgraphen, wie er in sozialen Plattformen zu finden ist, werden wir mit diesem Artikel versuchen, uns einer bestimmten Klasse von Datenstrukturen zu nähern und eine vergleichsweise einfache Lösung des Problems zu entwickeln.
Im Folgenden werden wir den Begriff der persistenten Datenstruktur verwenden. Er ist nicht zu verwechseln mit dem Persistenzbegriff aus der Datenhaltung. Man versteht darunter eine Datenstruktur mit Lese- und Update-Operationen und der Eigenschaft, dass alle Update-Operationen die alte Version der Datenstruktur zusätzlich zur Verfügung stellen. Das erlaubt uns, auch nach einem Update noch in die Vergangenheit zu blicken und alle alten Zustände, also die komplette Historie der Datenstruktur einzusehen.
Neben dieser Rückblick-Funktionalität erlauben persistente Datenstrukturen vor allem, ohne destruktive Update-Operationen zu arbeiten. In einem vorigen Artikel haben wir erklärt, warum eine solche Programmierweise einfacher zu verstehen ist und einfacher zu korrektem und besser wartbarem Code führt. Die Minimierung von Seiteneffekten bietet zudem enorme Vorteile für die Parallelisierbarkeit.
Wir wollen uns nun unserem Anwendungsbeispiel zuwenden: Als Programmiersprache verwenden wir hier beispielhaft C++11, die Ideen sind aber komplett sprachunabhängig und universell einsetzbar. Insbesondere soll damit einmal mehr gezeigt werden, dass Konzepte aus der funktionalen Programmierung durchaus auch in imperativen Sprachen nützlich sein können.
Unsere Aufgabenstellung ist die folgende:
- Verwalte einen Freundschaftsgraphen mit Benutzern und Freundesbeziehungen.
- Stelle eine Funktion
get_friends(user)bereit, die die Freundesliste eines Benutzers zurückgibt. - Stelle eine Funktion
add_friendship(user1, user2)bereit, die eine (einseitige) Freundschaftsbeziehung einleitet. - Erlaube den Zugriff auf alte Versionen des Graphen möglichst effizient.
Zunächst stellt sich natürlich die Frage, wie wir ganz unabhängig von jeglichem Zeitreisen unseren Graphen im Speicher repräsentieren wollen. Wir werden dazu unsere (n) Benutzer von (0) bis (n - 1) durchnummerieren und eine Adjazenzlistendarstellung verwenden. Eine ganz einfache Implementierung, die noch keine Versionierung unterstützt, könnte zum Beispiel wie folgt aussehen:
// Typalias: Eine Liste befreundeter Benutzer
typedef vector<int> AdjList;
// bildet Benutzer auf ihre Freundeslisten ab
// z.B: friends_by_user[100] = Liste der Freunde von Benutzer Nummer 100
vector<AdjList*> friends_by_user;
// ein Helfer, der bestimmt ob ein Element in einem
// Array enthalten ist
bool contains(vector<int>& v, int x) {
return v.end() != find(v.begin(), v.end(), x);
}
void add_friendship(int a, int b) {
// ist a schon mit b befreundet?
if (!contains(*friends_by_user[a], b))
friends_by_user[a]->push_back(b);
}
vector<int>* get_friends(int a) {
return friends_by_user[a];
}
int main() {
// wir legen 10^6 Benutzer an
for (int i = 0; i < 1000000; ++i)
friends_by_user.push_back(new AdjList);
// wir fügen einige Freundschaftsbeziehungen hinzu
add_friendship(0,1);
add_friendship(0,2);
add_friendship(1,2);
// gib die Freunde von 0 aus
vector<int> friends_of_0 = *get_friends(0);
for (int i = 0; i < friends_of_0.size(); ++i)
cout << friends_of_0[i] << endl;
}Die Ausgabe fällt wie erwartet aus:
1
2
Diese Darstellung und die zugehörigen Funktionen stellen bereits die Basisfunktionalität zur Verfügung, die wir für unsere Anwendung benötigen. Unser nächstes Ziel ist es, diese Datenstruktur persistent zu machen.
Ein erster Versuch
Wir können eine einfache Art von Persistenz tatsächlich ganz einfach implementieren: Wir kopieren bei jedem Update die komplette Datenstruktur und verändern nur die Kopie. Der veränderte Code könnte dann z.B. so aussehen:
typedef vector<AdjList*> Graph;
AdjList* get_friends(Graph& g, int a) {
return g[a];
}
// legt eine neue Version des Graphen an
Graph* add_friendship(Graph& old, int a, int b) {
if (contains(*get_friends(old, a), b))
return &old;
// alten Graph kopieren (wir benutzen hier den Kopierkonstruktor!)
Graph* g = new Graph(old);
// Adjazenzlisten von a und b kopieren
(*g)[a] = new AdjList(*old[a]);
(*g)[a]->push_back(b);
return g;
}
void print_friends(Graph& g, int a) {
AdjList friends = *get_friends(g, a);
for (size_t i = 0; i < friends.size(); ++i)
cout << friends[i] << " ";
cout << endl;
}
int main() {
Graph g;
// bildet Versionsnummern auf Zustände des Graphen ab
vector<Graph*> versions;
// wir legen 10^6 Benutzer an
for (int i = 0; i < 1000000; ++i)
g.push_back(new AdjList);
// wir legen ein paar verschiedene Versionen an
versions.push_back(&g); // Version 0
versions.push_back(add_friendship(g, 0, 1)); // Version 1
versions.push_back(add_friendship(*versions[1], 0, 2)); // Version 2
versions.push_back(add_friendship(*versions[2], 2, 3)); // Version 3
// Freunde von 0 zum Zeitpunkt 1
print_friends(*versions[1], 0);
// Freunde von 0 zum Zeitpunkt 2
print_friends(*versions[2], 0);
}Diese Variante hat natürlich einen offensichtlich entscheidenden Nachteil: Wir können nun zwar in die Vergangenheit blicken, allerdings bezahlen wir einen hohen Preis: Unser Speicherverbrauch steigt rapide mit der Anzahl der Updates, da wir jedes mal ein Array kopieren, welches in seiner Größe linear in der Anzahl der Benutzer ist.
Es ist auch klar, dass das viel besser gehen muss, denn schließlich werden bei jedem Update nur genau ein Wert in diesem Array überhaupt verändert. Der Rest bleibt zwischen zwei Versionen exakt gleich.
Wir werden im Folgenden die Optimierung der Freundeslisten an sich vernachlässigen, da sie im Vergleich zu der großen Liste aller Benutzer wenig Speicher verbrauchen. Ähnliche Tricks können allerdings auch dort angewendet werden.
Auf der Suche nach einer speichereffizienteren Gestaltung ist nun ein Trick fast immer nützlich:
Indirektion
Im Moment hat unsere Datenstruktur zur Referenzierung der Freundeslisten genau eine Ebene, wir können also mit einer einzigen Pointeroperation auf die Freunde eines Benutzers zugreifen. Diese Forderung werden wir jetzt aufgeben. Wir entscheiden uns stattdessen dafür, unser Array in (k) gleichgroße Teile aufzuteilen (Level 2), welche wiederum von einem höhergeordneten Array der Größe (k) aus referenziert werden (Level 1):
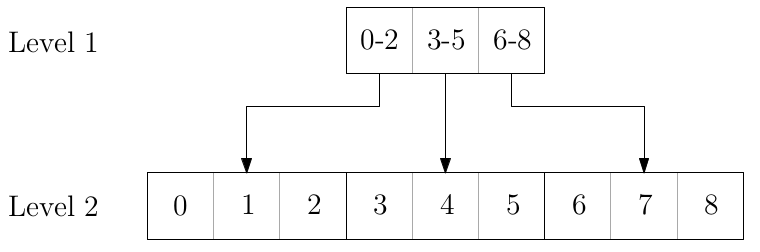
Klar ist, dass wir noch immer in konstanter Zeit Freundesabfragen machen können, wir benötigen diesmal eben zwei anstatt wie zuvor nur eine Pointerauflösung.
Interessanter ist die Frage, was wir bei einem Update nun alles tun müssen. Zunächst müssen wir den betroffenen Block im Level-2-Array kopieren. Wir müssen zudem das Level-1-Array kopieren, da sich die Zeiger auf die geänderten Blöcke ändern. Die Blockgröße beträgt ungefähr (\frac{n}{k}), insgesamt müssen wir also Speicher der Größenordnung (\mathcal{O}(k + \frac{n}{k})) kopieren.
Idealerweise wählen wir daher (k = \sqrt{n}), sodass bei jedem Update nur noch (\mathcal{O}(\sqrt{n})) Speicher kopiert werden muss. Da in unserem Beispiel (10^6) Benutzer vorkommen, entscheiden wir uns für die Blockgröße (1000):
const int BLOCK_SIZE = 1000;
typedef vector<AdjList*> GraphLevel2;
typedef vector<GraphLevel2*> Graph;
AdjList* get_friends(Graph& g, int a) {
// Indirektion auflösen
return (*g[a / BLOCK_SIZE])[a % BLOCK_SIZE];
}
Graph* add_friendship(Graph& old, int a, int b) {
if (contains(*get_friends(old, a), b))
return &old;
// kopiere Level 1
Graph* g = new Graph(old);
// kopiere Level 2
GraphLevel2* new_lvl2 = new GraphLevel2(*old[a / BLOCK_SIZE]);
// kopiere Adjazenzliste
AdjList* new_adjlst = new AdjList(*(*new_lvl2)[a % BLOCK_SIZE]);
new_adjlst->push_back(b);
(*new_lvl2)[a % BLOCK_SIZE] = new_adjlst;
(*g)[a / BLOCK_SIZE] = new_lvl2;
return g;
}
int main() {
Graph g;
// bildet Versionsnummern auf Zustände des Graphen ab
vector<Graph*> versions;
// wir legen 10^6 Benutzer an
for (int i = BLOCK_SIZE; i > 0; --i) {
GraphLevel2* block = new GraphLevel2;
for (int j = BLOCK_SIZE; j > 0; --j)
block->push_back(new AdjList);
g.push_back(block);
}
// der Rest bleibt genau gleich
}Wir haben nun also durch die Indirektion sowohl die Update-Zeit als auch den Speicherverbrauch unserer Datenstruktur um den Faktor (\sqrt{n}) verbessert, ohne die konstante Zugriffszeit auf die Freundesliste zu beeinflussen. Ein echter Erfolg! Aber können wir es noch besser?
Mehr Indirektion
Die Frage drängt sich beinahe auf: Warum genau eine Ebene an Indirektion? Warum nicht zwei oder drei oder (m)? Tatsächlich können wir eine beliebige (feste) Anzahl an Ebenen (m) wählen, sodass Updates mit Laufzeit und Speicheroverhead (\mathcal{O}(m \cdot n^{\frac{1}{m}})) möglich sind und trotzdem noch konstante Zugriffszeiten zusichern.
An dieser Stelle wird uns klar, dass die simple Datenstruktur, die wir entworfen haben, es uns tatsächlich ermöglicht, die gesamte Historie unseres Graphen in einer effizienten Art und Weise zu speichern. Wir können sogar noch mehr: Wir können auch Update-Operationen auf alten Versionen der Datenstruktur ausführen und damit untersuchen, was passiert wäre, wenn… In unserer Zeitreisenanalogie wäre das dann vergleichbar mit dem Schaffen eines Paralleluniversums.
Noch mehr Indirektion
Denkt man unseren bisherigen Ansatz noch weiter, kommt man vielleicht auf die Idee, nicht eine konstante Anzahl von Ebenenen zu verwenden, sondern eine Zahl in Abhängigkeit von (n). Für (m = \log_2 n) erhält man interessanterweise einen ganz normalen Binärbaum mit Update und Zugriff in (\mathcal{O}(\log n)), der dann natürlich automatisch persistent ist. Beim Update kopieren wir dabei alle Knoten auf dem Weg von der Wurzel zum Blatt genau einmal.
„Echte“ Implementierungen von persistenten Arrays, wie sie hier kurz vorgestellt
wurden, benutzen verschiedene Kompromisse und Tricks, um die Laufzeit der wichtigen
Operationen in der Realität möglichst gering zu halten. Als Beispiel sei hier auf
die Clojure-Implementierung von PersistentVector
verwiesen, die mit (m = \log_{32} n) arbeitet und damit die
Parallelverarbeitung der CPU auf Wortebene und auch den schnellen CPU-Cache optimal
ausnutzt.
Ausblick
Natürlich lassen sich nicht nur Graphdatenstrukturen persistent implementieren. Praktisch alle wichtigen Datenstrukturen, wie Listen, sortierte Folgen, Suchbäume und hashbasierte assoziative Datenstrukten besitzen persistente Analoga. Sie kommen vor allem in funktionalen Sprachen zum Einsatz.
Für weitere Informationen dazu sei zum Beispiel auf einen Blogartikel von Debasish Ghoshs verwiesen und auf die exzellente Vorlesung von MIT-Professor Erik Demaine zum Thema persistente Datenstrukturen.
Den gesamten Code der oben gezeigten Beispiele kann natürlich wie immer zum Ausprobieren heruntergeladen werden!