In
einem vorigen Beitrag
haben wir aus einzelnen Schnecken eine Schneckenwelt
zusammengesetzt und grafisch dargestellt. Bisher haben sich die
Schnecken einfach nur stur in gerader Linie bewegt; in diesem
Posting wollen wir es etwas interessanter machen und jede Schnecke mit
einer Schleimspur ausstatten, und schließlich dafür sorgen, daß
andere Schnecken dieser Schleimspur ausweichen. („Der Schleim der
anderen Schnecken stinkt!“) Am Ende soll das dann so aussehen:
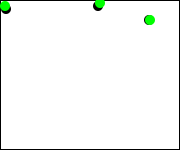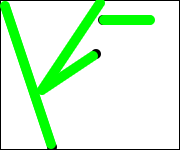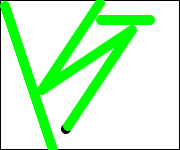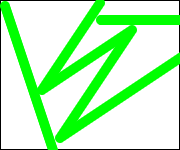
</img>
Diese Erweiterungen verdeutlichen weitere Vorteile der rein
funktionalen Programmierung:
-
Die explizite Angabe von Abhängigkeiten macht Zusammenhänge zwischen
Werten im Programm deutlich und dessen Bedeutung unabhängig von der
Auswertungsreihenfolge.
-
Der explizite Umgang mit Zeit ermöglicht eine akkurate Simulation
der Schneckenwelt.
-
Der explizite Umgang mit Identität macht Programme weniger
fehleranfällig und einfacher zu debuggen gegenüber imperativen
Programmen.
Um den Schleim zu repräsentieren, schreiben wir eine Daten- und eine
Record-Definition
für Schleim. Die Schleimspur hat eine feste Position … und sie ist
einer bestimmten Schnecke zugeordnet. (Wenn eine Schnecke auch ihrem
eigenen Schleim ausweichen würde, würde es problematisch mit der
Bewegung werden, da der Schleim unter der Schnecke entsteht.) Der erste
Versuch einer Definition für Schleimspuren könnte also so aussehen:
; Eine Schleimspur besteht aus:
; - der zugehörigen Schnecke
; - der Position der Schleimspur
(struct slime (snail pos))
Die Annahme dieser Definition ist natürlich, daß das snail-Feld in
der Schleimspur ein Schneckenobjekt wie aus den letzten beiden Folgen
ist, dessen Definition diese hier ist:
; Eine Schnecke hat:
; - Position
; - Bewegungsrichtung
(struct snail (pos dir))
Das Problem mit der Idee ist, daß ein snail-Objekt nur ein
Schnappschuß einer Schnecke zu einer bestimmten Zeit ist. Mit
anderen Worten: Wenn die Schnecke sich bewegt - neues Schneckenobjekt.
Dieses Objekt taugt also nicht, um eine Schleimspur einer bestimmten
Schnecke zuzuordnen, u.a., weil sie dann den eigenen Schleim aus der
Vergangenheit nicht mehr als ihren eigenen erkennen würde. Wir wollen
aber die Schleimspur „der Schnecke im allgemeinen“ zuordnen - also
ihrer Identität. Eine Identität muß ein Wert sein, der die
Schneckenzustände durch die Zeit verbindet - und den wir mit anderen
Identitäten vergleichen können, um zu prüfen, ob sie zur selben
Schnecke gehören.
In imperativen Programmen wird für so etwas häufig die Objektreferenz
verwenden. In Java könnte das so aussehen:
class Snail {
Pos pos;
Delta dir;
}
class Slime {
Snail snail;
Pos pos;
// gehört diese Schleimspur zu jener Schnecke?
boolean belongsToSnail(Snail snail) {
return this.snail == snail;
}
}
Dieser Ansatz macht OO-Programme allerdings oft schwer zu debuggen, da
die Identität nicht direkt sichtbar gemacht werden kann. („Sind zwei
Schnecken an der gleichen Position dieselbe Schnecke?“)
In der rein funktionalen Programmierung ist es gar nicht möglich, die
Objektreferenz als Identität zu benutzen. Darum machen wir die
Identität explizit und stecken sie als zusätzliches Feld in jede
Schnecke:
; Eine Schnecke hat:
; - Identität
; - Position
; - Bewegungsrichtung
(struct snail (id pos dir))
Als Identität benutzen wir hier der Einfachheit halber eine Zahl,
müssen also die Beispiele entsprechend ergänzen:
(define s1 (snail 1 p1 d1))
(define s2 (snail 2 p2 d2))
(define s3 (snail 3 p3 d3))
Außerdem müssen wir dafür sorgen, daß, wenn die Schnecke sich bewegt,
die Identität erhalten bleibt:
(define move-snail-in-dir
(lambda (s d)
(snail (snail-id s)
(move (snail-pos s) d)
d)))
Das Identität können wir jetzt in einer revidierten Definition für
Schleimspuren benutzen:
; Eine Schleimspur besteht aus:
; - der Identität der zugehörigen Schnecke
; - der Position der Schleimspur
(struct slime (id pos))
Die Schleimspur malen wir sehr ähnlich der Schnecke selbst als Kreis -
selbstverständlich als grünen Kreis:
(define draw-slime
(lambda (sl scene)
(let ((p (slime-pos sl)))
(place-image (circle snail-radius "solid" "green")
(pos-x p)
(pos-y p)
scene))))
An dieser Stelle ist es Zeit, das Konstrukt let zu erläutern: Es
bindet eine lokale Variable p an die Position des Schleims - die
dann mehrfach verwendet wird.
Wir brauchen dafür noch eine Hilfsdefinition für snail-radius, die
wir auch anderswo - beispielsweise in draw-snail - verwenden können:
; Radius einer Schnecke
(define snail-radius 5)
Jetzt müssen wir die Schleimspuren noch in der Schneckenwelt
plazieren. Dazu erweitern wir die Definition des
snail-world-Records:
; Eine Schneckenwelt besteht aus:
; - Schnecken
; - Schleimspuren
(struct snail-world (snails slimes))
Für unser Beispiel fangen wir mit einer leeren Liste von Schleimspuren
an:
(define sw1 (snail-world (list s1 s2 s3) '()))
Um eine solche Schneckenwelt zu malen, müssen wir nach den Schnecken
auch noch die Schleimspuren malen:
; Schneckenwelt malen
; draw-snail-world: snail-world -> scene
(define draw-snail-world
(lambda (sw)
(let* ((sc1
(foldl draw-snail
(empty-scene width height)
(snail-world-snails sw)))
(sc2
(foldl draw-slime sc1
(snail-world-slimes sw))))
sc2)))
Das let* ist ähnlich let und macht zwei Bindungen von lokalen
Variablen hintereinander: sc1 ist die Szene mit den Schnecken drin,
in sc2 sind zusätzlich die Schleimspuren eingezeichnet.
Allerdings sind bisher noch keine Schleimspuren da, die wir
einzeichnen könnten. Wir müssen erst noch dafür sorgen, daß die
Schnecken tatsächlich welche hinterlassen. Dafür erweitern wir die
Funktion next-snail-world, die aus einer Schneckenwelt die nächste
berechnet - bisher, indem sie alle Schnecken bewegt hat. Wir erzeugen
für jede Schnecke an ihrer aktuellen Position ein
Schleim-Objekt. Nehmen wir an, die Liste der Schnecken sei snails,
dann bekommen wir eine Liste der Schleimspuren so:
(map (lambda (s)
(slime
(snail-id s) (snail-pos s)))
snails)
Hier benutzen wir die eingebaute Funktion map: map akzeptiert eine
Funktion und eine Liste - sie wendet die Funktion auf jedes
Listenelement einzeln an und macht aus den Ergebnissen wieder eine
Liste. Hier lassen wir map auf die Liste der Schnecken los und
wenden die Funktion (lambda (s) ...) aus jedes Element an - diese
macht aus Schneckenidentität und -position eine Schleimspur. Heraus
kommt also eine Liste der Schleimspuren.
In der fertigen Version von next-snail-world müssen wir zusätzlich
zu den neuen Schleimspuren auch noch die alten Schleimspuren
herüberretten. Das Ergebnis sieht dann so aus:
; Schneckenwelt bewegen
; next-snail-world: snail-world -> snail-world
(define next-snail-world
(lambda (sw)
(let ((snails (snail-world-snails sw)))
(snail-world
(map move-snail snails)
(append (map slime
(map snail-id snails) (map snail-pos snails))
(snail-world-slimes sw))))))
Das Programm liefert jetzt immerhin schon dieses Ergebnis:
</img>
Allerdings war ja noch geplant, daß die Schnecken den Schleimspuren
anderer Schnecken ausweichen: Die Funktion move-snail muß noch den
Schleim berücksichtigen und gegebenenfalls die Richtung ändern. Dafür müssen
wir erst einmal die Signatur von move-snail um die Liste der
Schleimspuren erweitern:
; move-snail: snail (list-of slimes) -> snail
(define move-snail
(lambda (s slimes)
...))
Bisher wurde im Rumpf einfach die Schnecke in der Bewegungsrichtung
bewegt:
(move-snail-in-dir s (snail-dir s))
Das geht jetzt unter Umständen nicht mehr, wenn in der Bewegungsrichtung Schleim
liegt. Das müssen wir erst einmal feststellen. Dazu definieren wir
eine Hilfsfunktion slime-in-direction?, die feststellt, ob in einer
bestimmten Richtung von der Schnecke aus gesehen Schleim ist. Die
Funktion nimmt sich jede Schleimspur einzeln vor:
; Liegt Schleim in einer bestimmten Richtung von der Schecke?
; slime-in-direction?: snail (list-of slime) delta -> boolean
(define slime-in-direction?
(lambda (s slimes d)
(ormap (lambda (sl)
(and (not (equal? (snail-id s) (slime-id sl)))
(pos-in-slime? (move (snail-pos s) d) sl)))
slimes)))
Hier wird die eingebaute Funktion ormap verwendet, die - ähnlich
wie map - eine Funktion auf alle Elemente losläßt. In diesem Fall
muß die Funktion allerdings einen booleschen Wert zurückliefern.
ormap macht dann ein boolesches Oder über die Rückgabewerte für alle
Elemente - sobald eines „true“ ergibt, liefert auch ormap „true“.
In diesem Fall suchen wir ja nach einer Schleimspur, die zwei
Kriterien erfüllt:
- sie gehört zu einer anderen Schnecke
- die Position der Schnecke - um
d bewegt - liegt in der Schleimspur
Genau dieses Kriterium testet die Funktion, die an ormap übergeben
wird. Die eingebaute Funktion equal? testet zwei Identitäten auf
Gleichheit. Die Hilfsfunktion pos-in-slime? testet, ob eine
Position innerhalb einer Schleimspur liegt. (Ihre Definition ist
nicht besonders interessant, darum drucken wir sie nicht ab.)
Schließlich müssen wir move-snail noch vervollständigen. Diese
Funktion muß ggf. die Bewegungsrichtung ändern. Dazu brauchen wir
eine ganze Liste alternativer Richtungen zu einer
Bewegungsrichtung. Für die Berechnung einer solchen Liste benutzen
wir eine (ziemlich willkürlich definierte) Hilfsfunktion, die eine
Liste solcher Richtungen produziert:
; Alternative Richtungen zur Bewegungsrechnung berechnen
; alternative-directions: delta -> (list-of delta)
(define alternative-directions
(lambda (d)
(let ((dx (delta-x d))
(dy (delta-y d)))
(list (delta dx dy)
(delta dy dx)
(delta (- dx) dy)
(delta dx (- dy))
(delta (- dx) (- dy))
(delta (- dy) dx)
(delta dy (- dx))
(delta (- dy) (- dx))))))
Mit ihrer Hilfe können wir move-snail vervollständigen:
(define move-snail
(lambda (s slimes)
(let ((d
(ormap (lambda (d)
(if (slime-in-direction? s slimes d)
#false
d))
(alternative-directions (snail-dir s)))))
(if d
(move-snail-in-dir s d)
s))))
Wieder benutzen wir ormap, diesmal, um über alle möglichen
Alternativrichtungen zu iterieren und eine Richtung zu suchen, in der
kein Schleim ist. Falls die Funktion im ormap-Aufruf eine Richtung
findet, in der kein Schleim ist (gut!), dann liefert sie diese
Richtung, sonst #false. Diese Richtung wird dann auch von ormap
zurückgegeben. Im darauffolgenden if wird dann getestet, ob das
ormap eine mögliche Bewegungsrichtung produziert hat - wenn nicht,
bleibt die Schnecke stehen.
Wir müssen im Aufruf von move-snail auch noch die Schleimspuren
unterbringen:
(define next-snail-world
(lambda (sw)
(let ((snails (snail-world-snails sw))
(slimes (snail-world-slimes sw)))
(snail-world
(map (lambda (s)
(move-snail s slimes))
snails)
...))))
Fertig!
Wenn Sie jetzt auf das entstandene Programm zurückblicken, ist Ihnen
vielleicht gar nicht mehr klar, welche Vorteile die rein funktionale
Programmierung hier bringt. Aber schauen Sie noch einmal move-snail
an: Die Funktion bewegt nur eine einzige Schnecke, nimmt dabei aber
Bezug auf die sie umgebende Schneckenwelt über die Liste slimes.
Diese Liste ist für alle Schnecken gleich: Alle Schnecken treffen ja
ihre Bewegungsentscheidung gleichzeitig.
In einem imperativen Programm würde aber move-snail einerseits die
Position der Schnecke in situ verändern. Dabei würde wohl auch eine
weitere Schleimspur erzeugt. Das hieße aber, daß es eine Rolle
spielt, in welcher Reihenfolge die Schnecken sich bewegen, weil jede
den Effekt der Bewegung der vorigen Schnecke sehen könnte. Diese
Reihenfolge entspricht aber nicht der „realen Welt“, die hier
simuliert wird, in der die Dinge gleichzeitig und koordiniert
ablaufen. Solche Koordination von gleichzeitigen Veränderungen ist in
objektorientierten imperativen Programmen außerordentlich schwierig,
während wir im rein funktionalen Programm darüber kaum nachdenken
müssen.
Es gibt noch weitere Vorteile:
-
Dadurch, daß alle Abhängigkeiten zwischen Werten durch den Datenfluß
explizit aufgeschrieben sind, ist die Reihenfolge der Auswertung
weitestgehend egal. Es kann also keine Fehler dadurch geben, daß
zwei Anweisungen vertauscht oder parallel ausgeführt werden, was in
imperativen Programmen häufig schwer zu findende Fehler produziert.
-
Es ist viel einfacher, Unit-Tests (und andere Tests, beispielsweise
spezifikationsgetriebene
Tests) zu schreiben, da
reine Funktionen nur die richtige Eingabe bekommen müssen, um die
richtige Ausgabe zu produzieren: Es ist nicht nötig, aufwendig einen
definierten Zustand zu erzeugen bzw. nach erfolgtem Test
wiederherzustellen.
-
Die explizite Repräsentation von allem erleichtert das Debugging,
da Zwischenzustände Objekte sind, die inspiziert und ausgedruckt
werden können.
Auf der anderen Seite ist die rein funktionale Programmierung manchmal
umständlich: Häufig muß Zustand durch das Programm „gefädelt“ werden,
wie hier die Schneckenwelt. Aber hierfür gibt es Abhilfe:
Monaden, über die Sie
anderswo im
Blog
eine Einführung finden.
Ich hoffe, der Artikel hat etwas die Arbeitsweise bei der rein
funktionalen Programmierung erläutern und diese etwas schmackhaft
machen können. Ich wünsche viel Spaß und Erfolg beim Einsatz in Ihrer
eigenen Software!
Den vollständigen Code können Sie übrigens
hier herunterladen.