Clojure hat sich als alternative Programmiersprache auf der JVM fest etabliert: Die Sprache ist ausgereift, das Ökosystem enthält viele nützliche Libraries und Frameworks, und die kleine aber rege Community ist freundlich und stellt viele Konferenzen und Meetups auf die Beine.

Nicht nur Clojures Nische ist klein: die Programmiersprache selbst ist es auch, und damit schnell und leicht erlernbar. Was ist die Anziehungskraft dieser winzigen Sprache gegen den Goliath Java?

Zwei Dinge sind da besonders relevant: Clojure-Programme sind kompakter als ihre Java-Pendants und ermöglichen damit die Konzentration auf das Wesentliche. Wichtiger noch: Clojure ist eine funktionale Sprache und ermöglicht damit oft eine andere Sicht auf die Domäne als das klassisch objektorientierte Java. Dieser Artikel demonstriert das anhand einer kleinen domänenspezifischen Sprache für Bilder. Vorkenntnisse in Clojure sind für die Lektüre nicht notwendig, die verwendeten Konstrukte werden allesamt erläutert.

Bilder als Objekte

Dieser Abschnitt erläutert den Übergang von der üblichen objektorientierten zur funktionalen Programmierung. Es soll also um Bilder gehen. Aus Sicht der objektorientierten Programmierung sollte aus jedem Substantiv in einer Domänenbeschreibung ein Objekt werden: Ein Bild sollte demnach durch ein Objekt repräsentiert werden.

Exemplarisch ist das zum Beispiel in Java-AWT so, wo es ein Interface java.awt.image.Image gibt, mit der relevanten Implementierung BufferedImage. Diese Klasse hat zum Beispiel diese Methode:

void setRGB(int x, int y, int rgb)

Sie setzt also in einem Raster aus Pixeln einen Pixel auf eine bestimmte Farbe. Ein BufferedImage ist also zunächst noch gar nicht das gewünschte Bild: das entsteht erst noch durch eine Folge von Methodenaufrufen, welche die Farbe bestimmter Pixel ändert. Die Idee „ein Bild besteht aus rechteckig angeordneten Pixeln jeweils bestimmter Farbe“ ist sehr technisch.

Die funktionale Programmierung beantwortet die Frage „Was ist ein Bild?“ auf höherer Ebene. Wenn Menschen ein Bild betrachten, so sehen sie an jeder Stelle des Bildes eine bestimmte Farbe. Das Konzept des „Pixels“ nehmen Menschen nicht direkt wahr. Die Idee „an jeder Stelle des Bildes eine bestimmte Farbe“ lässt sich aber auch ganz ohne Pixel formulieren, nämlich als eine Funktion von „Stelle“ zu „Farbe“. Diese Idee verfolgt das System Pan, das der prominente funktionale Programmierer Conal Elliott 2003 veröffentlichte. Dieser Artikel zeichnet seine Idee vereinfacht in Clojure nach.

Den Anfang macht die Datenmodellierung: Die Begriffe „Stelle“ und „Farbe“ müssen modelliert werden, bevor es so richtig losgeht. Eine „Stelle“ wird als kartesische Koordinaten mit x- und y-Feldern modelliert. In Clojure sieht das so aus:

(defrecord Point [x y])

Man kann schon sehen, dass Clojure ein Lisp-Dialekt ist, das heißt zusammengehörende Konstrukte immer von Klammern umschlossen sind. Das defrecord kennzeichnet die Definition eines Records, also eines Typs für zusammengesetzte Daten mit x- und y-Feld. In Java wäre das ein „Plain Old Java Object“, und in der Tat erzeugt Clojure für die obige Deklaration eine POJO-Klasse dafür namens Point mit x- und y-Feldern.

Die Record-Deklaration zeigt, dass Clojure eine dynamisch getypte Sprache ist: Man muss bei x und y nicht angeben, welche Typen sie haben, die werden erst zur Laufzeit entschieden. Für Koordinaten werden natürlich hier immer Zahlen verwendet.

Der Konstruktor von Point heißt in Clojure ->Point (also mit Pfeil vor dem Namen), und entsprechend sieht die Konstruktion eines Punkts zum Beispiel so aus:

(->Point 1 2)

Zwei Beispielpunkte namens point1 und point2 werden folgendermaßen definiert:

(def point1 (->Point 1 2))
(def point2 (->Point 0.5 4))

Für Point sind außerdem automatisch zwei Getter definiert mit den Namen :x und :y. Anders als in Java sind dies aber keine Methoden (die sind in Clojure eher verpönt), sondern Funktionen. Aufgerufen werden auch mit Klammern drum, wie folgt zum Beispiel:

• (:x point1) liefert 1
• (:y point2) liefert 4

Eine Farbe ist in diesem Artikel ein Boolean true oder false für schwarz respektive weiß. (Das ist leicht zu verallgemeinern auf beliebige Farben und Transparenz, macht aber diesen Artikel kürzer.)

Koordinaten und Farben sind also definiert: Ein Bild ist eine Funktion, die für Koordinaten - ein Point-Objekt eine Farbe liefert - true oder false. Hier ist ein Beispiel:

(defn vstrip
  [p]
  (<= (Math/abs (:x p)) 0.5))

defn definiert in Clojure eine Funktion, in diesem Fall eine, die vstrip heißt und - in eckigen Klammern - einen Parameter namens p hat. In Clojure - da es eine funktionale Sprache ist - liefert jede Funktion einen Wert, darum wäre return redundant: Die Funktion liefert also das Ergebnis eines Vergleichs mit <=. Hier sieht man, dass auch <= nur eine Funktion in Clojure ist und entsprechend vor die Argumente und mit Klammern drum geschrieben wird. Math/abs ist die statische Java-Methode aus der Math-Klasse. Die Funktion liefert also true, wenn die X-Koordinate von p zwischen -0,5 und +0,5 liegt, sonst false.

Um herauszubekommen, welche Farbe an bestimmten Koordinaten sitzt, kann vstrip einfach aufgerufen werden:

• (vstrip (->Point 0 0)) liefert true (schwarz)
• (vstrip (->Point 0.6 0)) liefert false (weiß)

Das Bild sieht entsprechend so aus:

… also genauer gesagt, ein Ausschnitt des Bildes von jeweils -2 bis +2, denn das Bild ist zumindest konzeptuell unendlich groß.

vstrip ist ziemlich langweilig. Marginal interessanter ist das hier:

(defn vstripes
  [p]
  (even? (int (Math/floor (:x p)))))

Die Funktion int macht ein Integer aus dem double, das bei Math/floor herausgekommen ist, und die Funktion even? testet, ob ein Integer gerade ist oder nicht. Das Fragezeichen gehört in Clojure zum Namen und ist Konvention für Funktionen, die ein Boolean liefern - in Java würde die Funktion isEven heißen.

Die gleiche Idee lässt sich auch in der Horizontalen verwirklichen:

(defn hstripes
  [p]
  (even? (int (Math/floor (:y p)))))

Weg vom Gefängnismuster geht es mit einer Tischdecke:

(defn checker
  [p]
  (even? (+ (int (Math/floor (:x p))) (int (Math/floor (:y p))))))

So ein bißchen kann man schon sehen, wo der Unterschied zwischen der objektorientierten Herangehensweise von java.awt.image.Image und diesem funktionalen Modell liegt: java.awt.image.Image ist geprägt durch eine Implementierungsidee (Pixel), während die funktionale Sicht auf der „mathematischen Essenz“ der Idee eines Bildes beruht. Zur Implementierung - wie also aus der Darstellung ein Bild auf dem Bildschirm wird - ist bisher noch gar nichts bekannt. (Aber keine Sorge, das kommt noch.)

Kombinatormodelle

Das Bild checker mit dem Schachbrettmuster wurde oben „direkt“ definiert. Aber checkers kann auch mit Hilfe von vstripes und hstripes definiert werden:

(defn checker
  [p]
  (not= (vstripes p) (hstripes p)))

Die Funktion not= testet auf „nicht gleich“, also effektiv ein Exklusiv-Oder auf den Farben von vstripes und hstripes. Das p wird von checker an vstripes und hstripes durchgeschleift: Die beiden Bilder werden also quasi als ganzes xor-kombiniert.

Diese Idee - zwei Bilder xor-kombinieren - kann man aus checker herausabstrahieren. Das sieht dann so aus:

(defn img-xor
  [img1 img2]
  (fn [p]
    (not= (img1 p) (img2 p))))

(Der Bindestrich gehört zum Namen - in Java würde man einen Underscore _ schreiben.)

Diese Funktion nimmt zwei Bilder - wie zum Beispiel vstripes oder hstripes als Argumente und liefert wieder ein Bild - also eine Funktion. Das fn ist das Clojure-Pendant zum Lambda-Ausdruck in Java und stellt eine Funktion her, die in diesem Fall ein Point-Objekt akzeptiert und eine Farbe liefert, mit dem gleichen Rumpf wie schon zuletzt bei checker. Das kann jetzt so definiert werden:

(def checker
  (img-xor hstripes vstripes))

… und damit ist sofort die Essenz von checker klar (hoffentlich), die bei der ersten Definition doch schwieriger zu sehen war.

Die Implementierung von Funktionen wie img-xor, die auf Bildern als ganzes operieren (sogenannte Kombinatoren), macht aus Clojure zusammen mit einer Library dieser Funktionen effektiv eine domänenspezifische Sprache.

Koordinatentransformation

Hier ist ein weiteres Bild:

Intuitiv kann man sehen, dass es eine ähnliche Idee wie checker umsetzt - nur irgendwie im Kreis statt im Quadrat. Ideal wäre, wenn gerade das Konezpt „im Kreis statt im Quadrat“ als Code ausgedrückt werden könnte. Und tatsächlich gibt es ja Koordinaten, die im Kreis statt im Quadrat funktionieren, sogenannte Polarkoordinaten. Die bestehen nicht aus X- und Y-Koordinate. Stattdessen stellt man sich vor, dass zu einem Punkt ein Strahl vom Ursprung gezeichnet wird. Die Polarkoordinaten sind dann die Länge des Strahls (auch der Radius, meist r) und der Winkel des Strahls zur X-Achse (meist ρ).

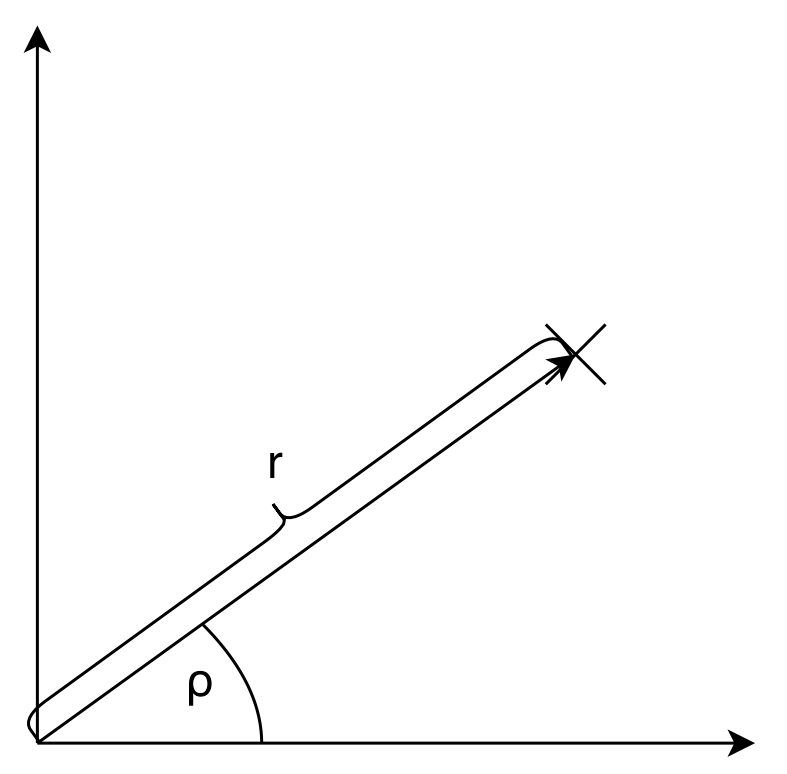
Das heißt, die kartesischen Quadratkoordinaten müssten nur in Polarkoordinaten umgerechnet werden. Das macht folgende Funktion, deren Formel man aus einer handelsüblichen Formelsammlung beziehen kann:

(defn to-polar
  [p]
  (->Point (distance-from-origin (:x p) (:y p))
           (Math/atan2 (:x p) (:y p))))

Die Hilfsfunktion distance-from-origin berechnet den Abstand vom Ursprung, ebenfalls mit einer Standardformel:

(defn distance-from-origin
  [x y]
  (Math/sqrt (+ (* x x) (* y y))))

Für das obige Bild wechselt die Farbe bei einer Kreisumdrehung insgesamt 20mal - also 10mal hin und zurück. Entsprechend muss der Winkel in den Polarkoordinaten angepasst werden, so dass eine Kreisumdrehung - zweimal Pi - gerade 20 entspricht. Das verallgemeinert folgende Hilfsfunktion turn, die bei Polarkoordinaten den Winkel (der im y-Feld steht) entsprechend skaliert:

(defn turn
  [n]
  (fn [p]
    (->Point (:x p)
             (* (:y p)
             (/ n Math/PI)))))

Die turn-Funktion akzeptiert also als Parameter n die Anzahl der Farbwechsel pro Umdrehung und liefert eine Funktion, die ein Point-Objekt entsprechend transformiert.

Um jetzt das Schachbrettmuster im Kreis zu bilden, müssen die Koordinaten zunächst mal mit to-polar in Polarkoordinaten umgewandelt und dann mit turn der Winkel skaliert werden, damit das ursprüngliche checker dann die Farbe ausrechnen kann. Die Koordinaten werden also durch eine kleine Pipeline geleitet, die aus drei Funktionen besteht. Mathematisch gesehen werden die Funktionen komponiert, darum heißt die eingebaute Funktion in Clojure dafür auch comp und wird so benutzt, um polar-checker zu definieren:

(defn polar-checker
  [n]
  (comp checker (turn n) to-polar))

Auch hier sieht man schön, wie die funktionale Sichtweise die Essenz der Idee dieses Bildes herausstreicht, und wie Clojure es erlaubt, die Idee in nur wenigen Zeilen Code zum Ausdruck zu bringen.

Mit etwas Sinn für Formelspielereien kann man so richtig hübsche Bilder machen. Zum Beispiel kann man auch umgekehrt von Polarkoordinaten in kartesische Koordinaten zurückrechnen:

(defn from-polar
  [p]
  (->Point (* (:x p) (Math/cos (:y p)))
           (* (:x p) (Math/sin (:y p)))))

(Auch diese Formel liefert die Formelsammlung.)

Das kann man benutzen, um auf den Polarkoordinaten Transformationen durchzuführen, indem die Koordinaten erst ins Polarformat überführt werden, dann transformiert, und dann in kartesische Koordinaten zurückgerechnet werden. Auch das ist eine Pipeline mit comp:

(defn from-polar-transformation
  [trafo]
  (comp from-polar trafo to-polar))

Die folgende Funktion bildet so den Kehrwert des Polarradius, stülpt also quasi innen nach außen:

(def invert-polar-radius
  (from-polar-transformation
   (fn [p]
     (->Point (if (zero? (:x p))
                0.0
                (/ 1.0 (:x p)))
              (:y p)))))

Das folgende Bild schaltet checker und ìnvert-polar-radius hintereinander:

(def rad-invert-checker
  (comp checker invert-polar-radius))

Der Aufsatz von Conal Elliott iefert noch mehr und schönere Beispiele, inklusive psychedelische Animationen.

Bilder auf den Bildschirm!

Die Essenz der Bilder ist schön und gut, aber trotzdem würde man sie natürlich gern sehen: Entsprechend geht es in diesem Abschnitt darum, zum Konzept die Implementierung zu liefern und demonstriert damit die andere Seite von Clojure, nämlich die Interoperatibilität mit Java.

Für die Darstellung der Bilder werden einige AWT- und Swing-Klassen benötigt, die in den Namespace importiert werden. Der Namespace ist das Clojure-Pendant zum Java-Package, und er wird am Beginn einer Dateil deklariert:

(ns javapro.functional-images
  (:import (java.awt Color Graphics Image BorderLayout)
           (javax.swing JFrame JLabel ImageIcon)
           java.awt.image.BufferedImage))

Damit kann die Funktion image->bitmap aus dem Clojure-Image eine handfeste Bitmap machen. Hier ist der Header dieser Funktion:

(defn image->bitmap
  [image width height x-min x-max y-min y-max]

Der Pfeil im Namen ist Konvention für Funktionen, die ein Objekt in ein anderes konvertieren. Bei den Parametern ist image das Clojure-Bild, width und height sind Höhe und Breite des Bildes in Pixel, und x-min, x-max, y-min und y-max sind der Koordinaten-Ausschnitt aus dem Bild, der angezeigt werden soll.

Als nächstes werden einige lokale Variablen gebunden, das geht in Clojure mit dem Konstrukt let: Dort stehen in eckigen Klammern die Namen lokaler Variablen und Ausdrücke für deren Werte, danach können die lokalen Variablen verwendet werden:

  (let [buffered-image (BufferedImage. 
                        width height
                        BufferedImage/TYPE_INT_ARGB)
        graphics (.getGraphics buffered-image)
        xinc (/ (- x-max x-min)
                (double width))
        yinc (/ (- y-max y-min)
                (double height))]

Für die erste Variable buffered-image erzeugt die Funktion ein BufferedImage-Objekt, in das die Funktion das Bild hineinmalen wird. Wie bei den Records ist BufferedImage. der Name des Konstruktors für diese Klasse. Danach wird aus buffered-image der Grafik-Context extrahiert - BufferedImage hat dafür die Methode getGraphics. Der Java-Aufruf dieser Methode buffered-image.getGraphics() wird in Clojure als Funktionsaufruf mit .getGraphics geschrieben.

Die beiden Bindungen für xinc und yinc rechnen schließlich aus, wie breit und wie hoch ein Pixel im Koordinatensystem des Bildes sind. (Die Funktion double macht aus den Integern width und height jeweils Doubles.)

Jetzt muss die Funktion über die Pixel des Bildes extrahieren, jeweils die Farbe ermitteln, diese im Grafik-Context als kleine Rechtecke malen und schließlich am Ende das BufferedImage-Objekt zurückliefern. Das doseq-Konstrukt ist das Pendant zum „foreach“ und Java und führt hier zwei geschachtelte Schleifen über alle Pixel des Bildes aus:

    (doseq [x (range 0 width)
            y (range 0 height)]
      (let [black? (image (->Point (+ x-min (* xinc x)) (+ y-min (* yinc y))))
            color (if black?
                    Color/BLACK
                    Color/WHITE)]
        (.setColor graphics color)
        (.fillRect graphics x y 1 1)))
    
    buffered-image))

Das Image-Objekt, das image->bitmap liefert, kann nun zum Beispiel in einem Fenster angezeigt werden mit folgender Funktion, die nahezu auschließlich aus Aufrufen von Java-Methoden besteht:

(defn display-image!
  [image width height x-min x-max y-min y-max]
  (let [bitmap (image->bitmap image width height x-min x-max y-min y-max)
        frame (JFrame. "Image")
        label (JLabel.)]
    (.setIcon label (ImageIcon. bitmap))
    (.setSize frame width height)
    (.setDefaultCloseOperation frame JFrame/EXIT_ON_CLOSE)
    (.add (.getContentPane frame) label BorderLayout/CENTER)
    (.pack frame)
    (.setVisible frame true)))

Fazit

Dieser Artikel konnte hoffentlich einen kleinen Einblick geben in die beiden Seiten von Clojure: Die eine Seite, die Domänenkonzepte in Reinform modelliert, und die andere Seite, die ihre Implementierung ermöglicht.

Natürlich ginge das alles auch in Java - allerdings mit einigen kleinen aber wesentlichen Abstrichen, die damit zu tun haben, dass Java zwar inzwischen Lambda-Ausdrücke aus der funktionalen Programmierung importiert hat, aber immer noch zwischen Methoden und Funktionen unterscheidet.

In Clojure hingegen kann die Idee des Domänenmodells in Reinform ausgedrückt werden, wobei ganz natürlich eine domänenspezifische Sprache entsteht. Dieser Prozess ist damit ein natürlicher Bestandteil der Arbeit mit Clojure, und Clojure kann dann auch die Implementierung des Konzepts und Anbindung an Betriebssystem und UI begleiten.

Die Sprache hat natürlich noch mehr zu bieten, ist aber insgesamt deutlich kleiner als Java und damit einfach zu beherrschen. Und, vor allem: Es macht viel mehr Spaß!