Einführung in Denotational Design, Teil I: Denotationelle Semantik

Dieser Artikel ist der Beginn einer Reihe über Denotational Design. In diesem Artikel geht es um die denotationelle Semantik. Im nächsten Artikel wenden wir die hier dargestellte Theorie auf ein Praxisbeispiel an.

Beim Programmieren wird viel Text produziert und dennoch ist Programmieren nicht gleich Textproduktion. Die Produktion von Text ist viel mehr die Form, in der etwas ganz anderes stattfindet, nämlich die Formulierung abstrakter Ideen in einer Sprache, die ein Computer behandeln kann. Der Computer kann sehr schnell Berechnungen ausführen, versteht selbst aber nicht, was er tut. Die Interpretation der Ein- und Ausgaben, das machen Menschen. Die Programmiercommunity fokussiert sich gern auf den Gesichtspunkt der Performance. Dieser ist durchaus wichtig, denn ohne Performance taugt die beste Software nichts. Etwas in Vergessenheit geraten ist dabei aber, dass es sich bei jeder Software lediglich um die Abbildung einer abstrakten Idee handelt. In dieser Artikelreihe wollen wir uns diesen abstrakten Ideen – wir sagen dazu oft: Modelle – und deren Verhältnis zum Computer widmen.

Das abstrakte Modell kommt spätestens immer dann zum Einsatz, wenn Bugs in der Software auftreten. Ein Bug, also ein Defekt in einem vorliegenden Programm, kann nur dann identifiziert werden, wenn man ein Idealbild vorm inneren Auge hat, mit dem man das defekte Programm vergleicht. Dass es diese abstrakte Idee – das Modell – hinter der Software also geben muss, sollte unstrittig sein.¹ Die Disziplin des Denotational Design rückt das Modell wieder in den Fokus und zeigt, wie dieses präzise beschrieben werden kann und wie diese Beschreibung in Einklang mit der Implementierung gebracht werden kann.

Denotationelle Semantik

In der Programmiersprachenforschung werden Programmiersprachen oft entlang der Semantik von Programmbausteinen studiert. Ein mögliches semantisches Werkzeug ist die denotationelle Semantik. Hierbei weist man jedem Datentyp eine mathematische Bedeutung zu, also einen Wert in der abstrakten Sprache der Mathematik: Mengen, Funktionen, Zahlen, Tupel etc. Operationen in der Programmiersprache werden definiert als (mathematische) Funktionen von den Bedeutungen der Argumente zu den Bedeutungen der Resultate.

Klingt abstrakt und ist es auch. Dahinter steckt aber wieder nur die Idee, dass jedes Programm eigentlich bloß eine konkrete Repräsentation einer abstrakten Idee ist. Die abstrakte Idee existiert in unseren Köpfen. Die zugehörige konkrete Repräsentation ist maßgeschneidert auf den Computer.

Das Original-Paper zur denotationellen Semantik erklärt diesen Gedanken anhand des Unterschieds zwischen Numeralen und natürlichen Zahlen. Die Sechs ist eine natürliche Zahl. Diese kann ich auf unterschiedliche Arten repräsentieren: „110“ in binär, „VI“ als römisches Numeral etc. Alle diese unterschiedlichen Repräsentationen (Numerale) meinen dieselbe Zahl. Mit einem einfachen Gleichungssystem kann eine Bedeutungsfunktion μ, die Numerale auf natürliche Zahlen abbildet, definiert werden. Für binäre Numerale:

𝛍(0) = 0
𝛍(1) = 1
𝛍(x0) = 2 * 𝛍(x)
𝛍(x1) = 2 * 𝛍(x) + 1

Die Bedeutungsfunktion 𝛍 beschreibt jetzt, was wir mit binären Numeralen „eigentlich meinen.“ An diesen Gleichungen sind einige Punkte bemerkenswert:

1. Die Bedeutungsfunktion 𝛍 bildet Numerale auf natürliche Zahlen ab. Die 0, die in den Klammern steht und die 0, die auf der rechten Seite steht, sind also unterschiedliche Objekte.
2. Das x ist kein Element der Numeralsprache, sondern eine Variable, die für beliebige Numeral(-teile) steht. Die dritte Gleichung und die vierte Gleichung beschreiben also eigentlich eine ganze Klasse von Gleichungen.
3. Die Definition von 𝛍 ist rekursiv, bezieht sich also für die Übersetzung eines Symbols rekursiv auf die Übersetzung eines Teilsymbols.
4. Diese Definition von 𝛍 hat einige Operationen als Voraussetzung. Auf der Seite der Numerale setzen wir voraus, dass es möglich ist, einzelne Ziffern aneinanderzukleben (x0). Auf der Seite der Zahlen gehen wir davon aus, dass wir multiplizieren und addieren können.

Der letzte Punkt ist beachtenswert, weil wir Multiplikation und Addition natürlich auch auf binären Numeralen definieren könnten. Das wäre zunächst etwas ganz anderes als die Operationen auf den natürlichen Zahlen. Wenn wir aber „Multiplikation und Addition auf binären Numeralen“ sagen, dann meinen wir wahrscheinlich Operationen, die auch den jeweiligen Operationen auf den natürlichen Zahlen entsprechen. Wir könnten das als Bedingung an korrekte Implementierungen formulieren:

𝛍(x + y) = 𝛍(x) + 𝛍(y)
𝛍(x * y) = 𝛍(x) * 𝛍(y)

Hier sagen wir, dass sich die Addition/Multiplikation auf Numeralen beobachtbar genau so verhalten sollen wie die Addition/Multiplikation auf natürlichen Zahlen. Das drücken wir über das Verhältnis der jeweiligen Ein- und Ausgaben der Operationen aus.

Anhand der einfacheren Inkrementieroperation inc können wir das Ganze durchspielen. Die Gleichung, die die Korrektheit regelt, lautet:

𝛍(inc(x)) = 𝛍(x) + 1

Achtung: inc ist eine ganz normale Operation auf Numeralen, bildet also Numeral auf Numeral ab. 𝛍 ist wie oben beschrieben eine besondere Funktion, die jedes Numeral auf eine natürliche Zahl abbildet. Wir können diesen Zusammenhang anhand eines Diagramms illustrieren.

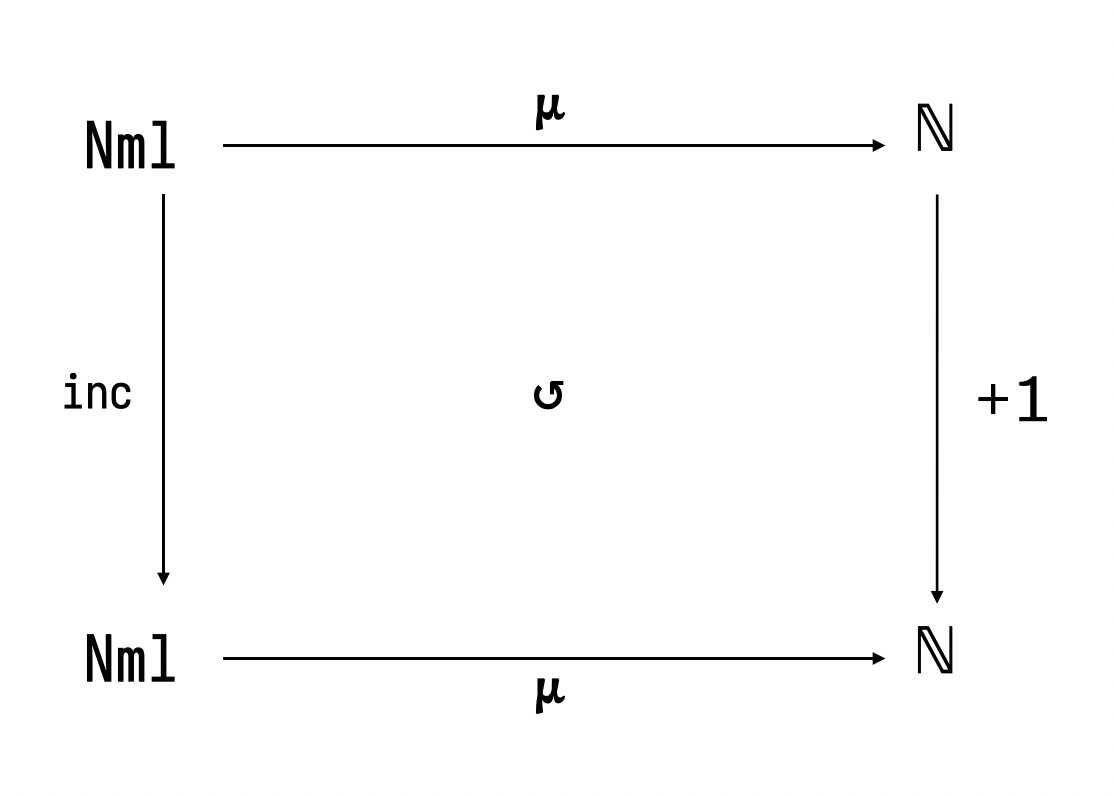
Dieses Diagramm können wir auf zwei Arten lesen: 1. +1 soll der Gegenspieler unserer Implementierung inc sein. D.h. für alle Paare von Numeralen, die inc als Eingabe und Ausgabe miteinander in Beziehung setzt, soll eine entsprechende Beziehung auch über +1 gelten, wenn man die Ein- und Ausgaben durch die Bedeutungsfunktion schickt. 2. Für alle Numerale als Eingabe für inc soll gelten: Es kommt am Ende die selbe Zahl raus, egal, ob man zunächst das Eingabenumeral in eine Zahl übersetzt und dann dort +1 rechnet, oder ob man zunächst inc anwendet und dann mithilfe der Bedeutungsfunktion diese Ausgabe in eine Zahl übersetzt. In jedem Fall handelt es sich bei diesen Überlegungen um ein Desiderat. Man spricht im Fall der Geltung dann von obigem Schaubild auch von einem kommutierenden Diagramm und inc wäre eine „korrekte Implementierung“ von +1².

Eine möglicherweise korrekte Implementierung für inc wäre jetzt:

inc(0) = 1
inc(1) = 10
inc(x0) = x1
inc(x1) = inc(x)0

Dass diese Implementierung korrekt ist, das ist bisher nur eine Behauptung. Diese Behauptung müssen wir noch beweisen, z.B. durch Induktion. Wir beginnen mit den beiden Basisfällen:

𝛍(inc(0)) = 𝛍(1) = 1 = 𝛍(0) + 1
𝛍(inc(1)) = 𝛍(10) = 𝛍(1) * 2 = 2 = 𝛍(1) + 1

Das passt. Weiter geht‘s mit dem Induktionsschritt:

// gegeben: 𝛍(inc(x)) = 𝛍(x) + 1

𝛍(inc(x0)) = 𝛍(x1)
           = 2 * 𝛍(x) + 1
           = 𝛍(x0) + 1

𝛍(inc(x1)) = 𝛍(inc(x)0)
           = 2 * 𝛍(inc(x))
           = 2 * (𝛍(x) + 1)
           = 2 * 𝛍(x) + 2
           = 2 * 𝛍(x) + 1 + 1
           = 𝛍(x1) + 1

Nun wissen wir, dass sich inc verhält wie + 1. Dieses Wissen hat eine ganz andere Qualität als die Sicherheit, die wir aus Tests kennen. Mit ausreichend vielen Tests (und im besten Fall sogar mit einigen Property Tests) können wir uns relativ sicher sein, dass unsere Implementierung korrekt ist. Hier wissen wir‘s.

Das ist ein subtiler Punkt, mit dem die ganze Angelegenheit aber steht und fällt. Was wissen wir denn genau? Dass sich inc auf den binären Numeralen so verhält wie + 1 auf den natürlichen Zahlen. Unter der Voraussetzung – aber nur unter der Voraussetzung – dass + 1 wirklich das ist, was wir implementieren wollten, ist unsere Software also korrekt. Das lässt noch offen, ob wir wirklich + 1 meinten, oder nicht doch + 2 oder was ganz anderes. Diesen letzten Schritt können wir nicht beweisen. Deshalb ist es wichtig, dass die Semantiken so simpel sind, dass sie auf einen Blick offensichtlich richtig sind.

Denotational Design

Die denotationelle Semantik entstand wie gesagt zur Erforschung von Programmiersprachen. Dieselbe Methode lässt sich aber ganz einfach auf beliebige zusammengesetzte Programmelemente übertragen. Wir wollen dies im nächsten Teil der Blogpostserie anhand von Zeitreihen illustrieren. Diese Gedanken kommen direkt aus einem großen Industrieprojekt aus unserer täglichen Arbeit. Ihr dürft also gespannt sein auf ein praxisnahes Fallbeispiel.