In Verbindung mit der funktionalen Programmierung taucht oft der
Begriff der rein funktionalen Programmierung auf. Die „Reinheit“
bezeichnet dabei den Verzicht auf Seiteneffekte, meist im besonderen den
Verzicht auf Zuweisungen an Variablen.
Entwicklern, die hauptsächlich in traditionellen objektorientierten
Sprachen zu Hause sind, erscheint diese Art der Programmierung oft
fremdartig und einschränkend - es geht ja schließlich erst einmal um
Verzicht. Wie Asketen wissen, erschließt Verzicht oft ungeahnte neue
Kräfte: Darum wird es auf diesem Blog später noch gehen. Dieser
Beitrag beschäftigt sich erst einmal damit, wie das überhaupt geht
mit der rein funktionalen Programmierung.
Zu diesem Zweck nehmen wir uns ein konkretes Beispiel vor: Es geht um
die Simulation und Visualisierung einer Welt (vielleicht für ein
Videospiel), in der sich Schnecken bewegen, entlehnt einer
Live-Coding-Session von der OOP 2013.
Die Schneckenwelt ist zweidimensional, und wir fangen mit sehr sturen
Schnecken an, die sich stets in die gleiche Richtung bewegen und sich
nicht davon abhalten lassen.
In diesem Posting kümmern wir uns erst einmal um die individuellen
Schnecken, die wir in einem späteren Posting dann in der Schneckenwelt
anordnen. In einem dritten Posting werden wir das Programm so
erweitern, daß die Schnecken Schleimspuren hinterlassen und den
Schleimspuren anderer Schnecken („die stinken“) ausweichen. Das ganze
visualisieren wir dann dergestalt, daß es so aussieht:
Wir programmieren das
ganze in Racket, das sich jeder
(inklusive einer wunderbaren IDE) kostenlos herunterladen kann, und
zwar für alle gängige Plattformen. Dieser Beitrag ist (hoffentlich)
auch eine brauchbare Einführung in die Grundelemente von Racket. Wir
benutzen außerdem die Prinzipien der
Konstruktionsanleitungen
bzw. design recipes.
Wir beginnen unser Programm mit einer Einleitung, die sagt, in welcher
der vielen bei Racket mitgelieferten Sprachen unsere Schneckenwelt
implementiert wird; wir nehmen die Standard-Racket-Basissprache:
#lang racket/base
Zu diesem Zweck beschreiben wir eine
Schnecke durch ihre Position und ihre Bewegungsrichtung. Fangen
wir also mit einer Datendefinition und einer Struct-Definition für
den Datentyp an:
; Eine Position besteht aus:
; - X-Koordinate
; - Y-Koordinate
(struct pos (x y))
Die
struct-Form
definiert Rackets Variante eines „Records“ (oder
„POJO“) mit zwei Feldern names x und y. Die Texte nach Semikolon
sind Kommentare.
Hier sind einige Beispiele für Positionen:
(define p1 (pos 5 6)) ; Position mit X=5, Y=6
(define p2 (pos 100 3)) ; Position mit X=100, Y=3
(define p3 (pos 150 20)) ; Position mit X=150, Y=3
Spätestens jetzt wird deutlich, daß Rackets Syntax sich an Lisp
anlehnt: Zusammengesetzte Formen werden immer durch Klammern
umschlossen, die Bestandteile werden durch Whitespace getrennt und am
Anfang steht immer ein „Operator“, der besagt, um was für eine Art
Form es sich handelt: bei struct um eine Record-Typ-Definition, bei
define um die Definition, also die Bindung eines globalen Namens an
einen Wert, und bei pos um die Konstruktion eines Positions-Werts.
Die Struct-Definition pos definiert einen Konstruktor gleichen
namens, der ein Argument für die X-Koordinate und eines für die
Y-Koordinate akzeptiert. Nach den obigen Definitionen stehen also die
Bezeichner p1, p2 und p3 für die entsprechenden Positionen.
Die Bewegungsrichtung repräsentieren wir durch ein Delta, das
analog zu Positionen definiert wird:
; Ein Delta besteht aus:
; - Delta in X-Richtung
; - Delta in Y-Richtung
(struct delta (x y))
(define d1 (delta 1 3)) ; Delta mit X=1, Y=3
(define d2 (delta -2 3)) ; Delta mit X=-2, Y=3
(define d3 (delta -1 0)) ; Delta mit X=-1, Y=0
Wir können nun einige Operationen auf Positionen und Deltas
definieren. Wir fangen an mit „bewege eine Position in eine
Richtung“, was wir auf jeden Fall für die Bewegung einer Schnecke
brauchen werden.
; Position in Richtung bewegen
; move: pos delta -> pos
(define move
(lambda (p d)
(pos (+ (pos-x p) (delta-x d))
(+ (pos-y p) (delta-y d)))))
Das lambda stellt eine Funktion her, mit zwei Parametern p und
d für die Position und die Bewegungsrichtung. Der Ausdruck im Rumpf
(pos ...) liefert den Rückgabewert der Funktion - kein return
o.ä. ist notwendig. In einer traditionellen objektorientierten
bzw. imperativen Sprache würde move wahrscheinlich die Werte der
x- und y-Komponenten der Position p einfach verändern, mit
Zuweisungen, die z.B. so aussehen könnten:
p.x = p.x + d.x;
p.y = p.y + d.y;
In der rein funktionalen Programmierung stellen die Funktionen in
solchen Situationen einfach neue Objekte her, in diesem Fall also eine
neue Position. Die alte bleibt unverändert. Wir hatten oben schon
gesehen, daß pos der Konstruktor für Positionen ist. Die
move-Funktion benutzt neben dem Konstruktor auch noch die
Selektoren pos-x, pos-y, delta-x und delta-y. Die
Selektoren sind Funktionen, die die entsprechende Komponente aus dem
Struct herausholen: (pos-x p) entspricht also p.x in Java. Der
Rumpf der obigen Funktion läßt sich also folgendermaßen lesen:
die Position, bei der die X-Komponente die Summe aus X-Komponente
von p und X-Komponente von d ist, und bei der die Y-Komponente
die Summe aus Y-Komponente von p und Y-Komponente von d ist
Kommen wir nun zu den Schnecken selbst. Oben war schon zu lesen, daß
eine Schnecke sich durch Position und Bewegungsrichtung auszeichnet:
; Eine Schnecke hat:
; - Position
; - Bewegungsrichtung
(struct snail (pos dir))
Hier einige Beispielschnecken:
(define s1 (snail p1 d1))
(define s2 (snail p2 d2))
(define s3 (snail p3 d3))
Die Schnecken sollen sich ja bewegen, also brauchen wir eine Funktion,
die eine Schnecke bewegt. Diese kann natürlich die schon definierte
move-Funktion benutzen. Wieder erzeugen wir eine neue Schecke,
anstatt in situ die alte Schnecke zu ändern:
; Schnecke in gegebene Richtung bewegen
; move-snail-in-dir: snail delta -> snail
(define move-snail-in-dir
(lambda (s d)
(snail (move (snail-pos s) d)
d)))
Schließlich können wir move-snail-in-dir benutzen, um eine Funktion
zu definieren, die eine Schnecke in ihre eigene Richtung bewegt:
; Schnecke in ihrer Richtung bewegen
; move-snail: snail -> snail
(define move-snail
(lambda (s)
(move-snail-in-dir s (snail-dir s))))
Manchen Lesern mag das unnatürlich vorkommen: Die Schnecke bewegt
sich doch, das heißt hinterher ist sie nicht mehr da, wo sie vorher
war! Das suggeriert, daß das imperative Modell - einfach die
Position ändern anstatt eine neue Schnecke herstellen - intuitiv
besser zur Realität paßt.
Das imperative Modell greift allerdings zu kurz: schließlich handelt
es sich bei einem snail-Objekt nicht um eine Schnecke, sondern die
Repräsentation einer Schnecke - und ihre Position ist, da die
Schnecke sich bewegt, immer nur die Position zu einer bestimmten
Zeit. Ein snail-Objekt ist also eine Momentaufnahme der Schnecke,
die sich nicht dadurch verändert, daß die Schnecke sich bewegt: Es
spricht nichts dagegen, daß ein Programm weiß, wo sich die Schnecke in
der Vergangenheit befundet hat. Häufig ist dieser Zugriff auf die
Vergangenheit sehr nützlich, wir werden aber in einem weiteren Posting
noch weitere Vorteile dieses Programmiermodells kennenlernen.
Zunächst einmal kümmern wir uns noch um die grafische Darstellung.
Dazu brauchen wir zwei Libraries, die bei Racket dabei sind -
2htdp/universe
und
2htdp/image.
Diese binden wir mit einer require-Form am Anfang unseres Programms
ein, unterhalb von #lang racket/base:
(require 2htdp/image)
Für die Anzeige der Schnecken benutzen wir
2htdp/image,
welche die rein funktionale Manipulation von Bildern erlaubt. Für die
Darstellung einer Schnecke benutzen wir einen einfachen Kreis:
(circle 5 "solid" "grey")
In einer herkömmlichen „Bilder-Mal-Library“ würde diese Funktion
wahrscheinlich einen Kreis in ein Bild hineinzeichnen. Hier ist das
anders:
circle
liefert ein komplettes Bild als Objekt, das sie
beliebig weiterverarbeiten können. Das können Sie nachvollziehen,
indem Sie obige Form in die DrRacket-REPL eintippen, das sieht dann so
aus:
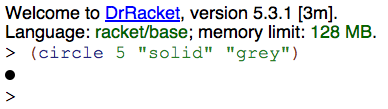 </img>
</img>
Für die Visualisierung der Schnecke in der Schneckenwelt müssen wir
den Kreis noch an der Position der Schnecke in einer Szene
plazieren. (Eine Szene ist auch nur ein Bild, aber die
terminologische Trennung zwischen Bild und Szene vereinfacht den
Umgang etwas.) Dafür schreiben wir eine Funktion draw-snail:
; Schnecke malen
; draw-snail: snail scene -> scene
(define draw-snail
(lambda (s scene)
(place-image (circle 5 "solid" "grey")
(pos-x (snail-pos s))
(pos-y (snail-pos s))
scene)))
Die Funktion
place-image
setzt also die Schnecke an ihrer eigenen
Position in die Szene hinein. In der REPL ist schön zu sehen, wie die
Funktion funktioniert:
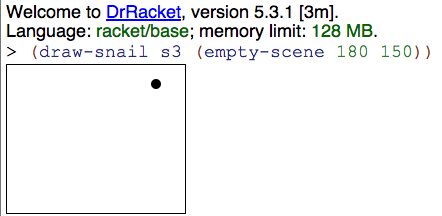 </img>
</img>
(Die
empty-scene-Funktion
macht eine leere rechteckige Szene mit der angegebenen Breite und Höhe.)
Für heute soll es erst einmal genug sein! Weiter geht es in Teil 2.
Den Code zu diesem Beitrag können Sie übrigens
hier herunterladen.