Computerprozessoren werden heutzutage nicht mehr mit jeder neue Generation
schneller und schneller. Stattdessen konzentrieren sich die Chiphersteller
darauf mehr Prozessorkerne in unsere Rechner einzubauen. Für die
Softwareentwicklung bedeutet dies dass Software nicht mehr automatisch mit
jeder Prozessorgeneration schneller läuft sondern dass die Entwickler
dafür etwas tun müssen.
Ein Zauberwort heißt daher parallele Programmierung. Damit ist gemeint
dass verschiedene Teile eines Programms gleichzeitg ablaufen können, somit
mehrere Prozessorkerne auslasten und im Endeffekt schneller an‘s Ziel
kommen. Die automatische Parallelisierung von Software ist allerdings
immer noch ein Traum; stattdessen muss Parallelität von Hand in die Software
eingebaut werden. Funktionale Programmierung eignet sich hervorragend zur
parallelen Programmierung, insbesondere weil funktionale Programme
diszipliniert und sparsam mit Seiteneffekten umgehen und damit ein großes
Hindernis für Parallelität von Grund auf vermeiden.
Dieser Artikel demonstriert, wie man in der funktionalen Sprache
Haskell sehr einfach und elegant parallele Programme
schreiben kann. Dazu stelle ich eine Haskell-Bibliothek vor, die Parallelität
ermöglicht ohne dabei auf ein deterministisches Programmverhalten zu verzichten.
Das bedeutet dass ein mit der Bibliothek entwickeltes paralleles Programm
garantiert dasselbe Ergebnis liefert, egal ob es auf einem, zwei oder 32
Prozessorkernen läuft (sofern das Programm keine anderen, nicht-deterministischen
Teile enthält).
In anderen Sprachen ist im Gegensatz dazu Parallelität häufig nicht-deterministisch.
Damit werden Programme deutlicher schwerer zu debuggen,
da sie beispielsweise auf einem Kern wunderbar funktionieren, auf zwei Kernen aber
das falsche Ergenbis berechnen und es auf vier Kernen hin und wieder
zu einem Deadlock kommt.
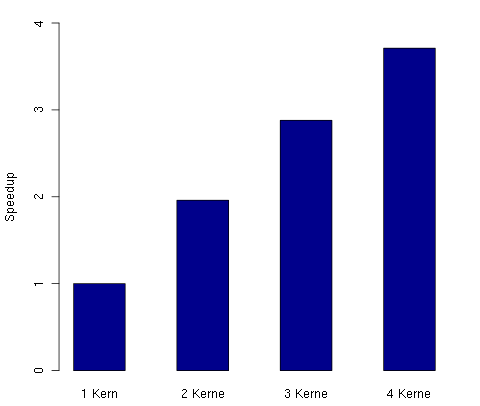
Als kleine Vorausblick hier der Speedup in Relation zur Anzahl der Kerne,
den wir mit Parallelität in Haskell
durch eine sehr einfache Modifikation eines ursprünglich sequentiellen Programms
erzielen können:
</img>
Zum Verständnis des Artikels sind Grundkenntnisse in Haskell sowie Bekanntschaft
mit der do-Notation hilfreich.
Bevor wir richtig loslegen, noch eine kurze Abgrenzung zwischen Parallelität
und Nebenläufigkeit. Wie oben geschrieben hat Parallelität zum Ziel ein
Programm schneller zu machen. Nebenläufigkeit hingegen ist eine inherente
Eigenschaft eines Programm und dient dazu, gleichzeitig mehrere
Interaktionen mit der Außenwelt führen zu können. Ein nebenläufiges Programm
ist damit zwangsläufig nicht-deterministisch, wohingegen parallele Programme
durchaus deterministisch sein können und es in diesem Artikel auch sind.
So, jetzt aber zu unserem konkreten Beispiel. Ich möchte in diesem Artikel
zeigen wie man in Haskell ein paralleles Programm zum Lösen von Sudokurätseln
entwickeln kann. Das Programm soll dabei auf beliebig viele Prozessorkerne
skalieren und die vorhandenen Kerne möglichst effizient ausnützen. Das gezeigte
Beispiel basiert auf einem Tutorial
von Simon Marlow. Ich habe den Code mit dem Glasgow Haskell Compiler
in Version 7.6.2 getestet.
In einem ersten Schritt schreiben wir ein sequentielles Programm. Wir
importieren zunächst das Modul Sudoko, welches eine Funktion solve
zum Lösen eines Sudokus bereitstellt. Da es in diesem Artikel nicht um Algorithmen
zum Lösen von Sudokurätsel geht und alle Parallelisierungsarbeit außerhalb
des Solvers stattfinden wird, spielt die eigentliche Implementierung des Sudoku-Moduls
keine Rolle. Außerdem importieren wir ein
spezielles Drivermodul
sowie ein Standardmodul.
-- Datei SudokuSeq.hs
import Sudoku
import Driver
import Data.Maybe
Das Drivermodul, dessen Implementierung an dieser Stelle irrelevant ist,
stellt eine Funktion driver zur Verfügung.
Diese Funktion übernimmt für uns das Parsen der Kommandozeilenargumente,
das Einlesen der Eingabedatei sowie das Extrahieren der einzelnen Rätsel
aus dieser Datei. Wir müssen driver lediglich mit einer Funktion zum
Lösen aller Sudokurätsel aufrufen. Die driver Funktion berechnet dann die
Lösungen und gibt die Anzahl der gelösten Rätsel aus.
Das restliche sequentielle Programme sieht dann wie folgt aus:
main = driver computeSolutions
where
computeSolutions puzzles =
filter isJust (map solve puzzles)
Das Argument puzzles von computeSolutions ist
eine Liste von Sudokurätseln.
Der Ausdruck map solve puzzles wendet die solve-Funktion auf jedes dieser Rätsel an.
Mit filter isJust können wir
aus der Ergebnisliste die echten Lösungen herausfiltern.
Jetzt können wir das Programm mit folgendem Befehl kompilieren:
ghc --make -O2 -threaded -rtsopts SudokuSeq.hs
Der komplette Code zu diesem Artikeln kann auch
heruntergeladen werden.
In dem .zip-Archiv befindet sich auch eine Datei sudoku17.1000.txt, welche 1000
Rätseln mit jeweils 17 vorbelegten Feldern enthält. Wenn wir nun das kompilierte
SudokuSeq mit dieser Datei aufrufen erhalten wir als Ausgabe tatsächlich 1000.
Da wir an der Laufzeit interessiert sind müssen wir dem Aufruf noch ein paar
extra Argumente spendieren:
./SudokuSeq +RTS -s -RTS sudoku17.1000.txt
Der Text zwischen +RTS und -RTS sind Parameter für das Laufzeitsystem. Damit
erhalten wir u.a. folgende Zusatzinformationen:
Total time 1.52s ( 1.53s elapsed)
Hier wird die gesamte CPU Zeit des Programms mit 1,52 Sekunden angegeben. Die komplette Laufzeit
(„wall time“) betrug 1,53 Sekunden. Nicht wirklich überraschend, schließlich handelt es sich um ein
sequentielles Programm.
Wir möchten nun dieses Programm parallelisieren. In Haskell stehen dazu mehrere Möglichkeiten
zur Verfügung. Wir beschäftigen uns in diesem Artikel mit einer Möglichkeit welche Parallelität
explizit einführt und Datenabhängigkeiten über spezielle Boxen repräsentiert.
Wenn Sie die folgenden Beispiel ausprobieren möchten, müssten Sie zunächst das
Paket monad-par installieren. Am einfachsten geschieht dies über den Befehl
cabal install monad-par-0.3
Nun zu unserer ersten Version des parallelen Sudoku-Solvers. Damit sie die Grundlagen
des monad-par Bibliothek besser kennenlernen, benutzt diese Version die Primitivoperationen
der Bibliothek. Wir werden dann in einer zweiten Version sehen, wie man das Problem
einfacher und effizienter mit von der Bibliothek bereitgestellten Abstraktionen lösen kann.
-- Datei SudokuPar1.hs
import Sudoku
import Driver
import Data.Maybe
import Control.Monad.Par
main = driver computeSolutions
where
computeSolutions puzzles =
let (as, bs) = splitAt (length puzzles `div` 2) puzzles
in runPar (do b1 <- new
b2 <- new
fork (put b1 (map solve as))
fork (put b2 (map solve bs))
res1 <- get b1
res2 <- get b2
return (filter isJust (res1 ++ res2)))
Um die Funktionalität des Pakets monad-par nutzen zu können ist der Import
von Control.Monad.Par hinzugekommen. Außerdem ist die Funktion computeSolutions deutlich
komplizierter geworden. Mittels splitAt teilen wir zunächst die Eingabe in zwei
etwa gleich große Teile as und bs auf. Auf diesen beiden Teilen soll
nun die Lösung parallel berechnet werden. Dazu bedienen wir uns folgender
primitiven Operationen aus dem Control.Monad.Par Modul:
-
new Legt eine neue „Box“ an in der später das Ergebnis einer parallelen Berechnung
gespeichert wird. Da wir zwei Berechnungen parallel ausführen möchten legen
wir zwei solcher Boxen b1 und b2 an.
-
put Speichert das Ergebnis einer Berechnung in einer Box. Damit parallele Berechnungen
deterministisch bleiben ist es verboten ein Ergebnis in eine volle Box zu schreiben.
-
get Holt das Ergebnis einer Berechnung aus einer Box. Falls die Box leer ist wartet
get solange bis ein Ergebnis vorliegt.
-
fork Stößt eine Berechnung an die dann parallel abläuft. In unserem Beispiel
benutzen wir fork um zwei parallele Berechnungen zu starten, die ihre Ergebnisse
in die Boxen b1 und b2 schreiben. Während die Berechnungen noch laufen
warten wir mittels get bis die Ergebnisse in b1 und b2 vorliegen.
-
runPar Um aus der Welt der parallelen Berechnungen das Ergebnis in die Welt der „normalen“
Haskell-Berechnungen zurückzureichen, müssen wir die parallele Berechnung auf oberster
Ebene in ein runPar einpacken.
Schauen wir uns nun mal die sequentielle Performance unserer ersten parallelen Version an.
Dies ist immer eine gute Prüfung um sich zu vergewissern, dass man nicht völligen
Blödsinn programmiert hat:
./SudokuPar1 +RTS -s -RTS sudoku17.1000.txt
Total time 1.52s ( 1.54s elapsed)
Wir erinnern uns, die sequentielle Version benötigt für denselben Benchmark insgesamt 1,53
Sekunden, es scheint also alles zu passen. Um nun mehrere Prozessorkerne zu verwenden
müssen wir dem Haskell Laufzeitsystem (RTS) die Option -N<K> mitgeben, wobei
<K> die Anzahl der Kerne ist:
./SudokuPar1 +RTS -s -N2 -RTS sudoku17.1000.txt
Total time 1.57s ( 0.97s elapsed)
Aha, jetzt brauchen wir nur noch 0,97 Sekunden anstatt 1,53 Sekunden im sequentiellen Fall.
Der Speedup berechnet sich wie üblich als Quotient dieser beiden Zeiten, also
1,53 / 0,97 = 1,55. Das ist leider nicht ganz das was wir erwartet haben, denn
da das Problem fast vollständig parallelisierbar ist sollte der Speedup bei zwei Kernen irgendwo
knapp unterhalb von 2 liegen.
Um dem Problem auf den Grund zu gehen erstellen wir während des Programmlaufs ein
Eventlog, das wir danach analysieren. Dazu müssen wir das
Programm mit der -eventlog Flag neu kompilieren
ghc --make -O2 -threaded -rtsopts -eventlog -o SudokuPar1_e SudokuPar1.hs
und dann mit der RTS Option -ls nochmals ausführen:
./SudokuPar1_e +RTS -s -N2 -ls -RTS sudoku17.1000.txt
Dann benutzen wir threadscope
um das damit erzeugte Eventlog SudokuPar1_e.eventlog
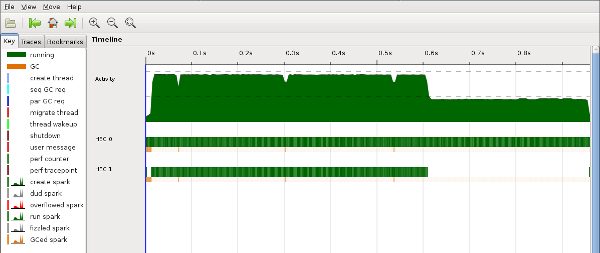
zu analysieren. Hier ist ein Screenshot des Hauptfensters von threadscope:
</img>
Richtig interessant am obigen Screenshot sind eigentlich nur die unteren beiden,
etwas dünneren, grünen Streifen. Diese zeigen die Aktivitäten der Prozessorkerne an.
Offensichtlich laufen die zwei Kerne nach einer kurzen Startphase schön parallel.
Aber nach etwas mehr als der Hälfte der Zeit geht einem Kern offensichtlich die Arbeit aus
und es ist nur noch ein Kern aktiv. Das Problem ist, dass
das Lösen zweier Sudokurätsel unterschiedlich lange dauern kann und dass unsere
Strategie, die Liste der Rätsel einfach in zwei Hälften zu teilen, diesen
Aspekt nicht berücksichtigt.
Schauen wir uns auch noch an was unsere erste parallele Version macht wenn wir ihr vier Kerne
zur Verfügung stellen:
./SudokuPar1 +RTS -s -N4 -RTS sudoku17.1000.txt
Total time 1.80s ( 1.03s elapsed)
Oh, die Performance ist sogar ein klein wenig schlechter geworden, obwohl meine Maschine
vier echte Kerne hat. Die etwas schlechtere Performance liegt am größeren Overhead
der durch die Verteilung auf mehrere Kerne entsteht.
Es sollte aber auch einleuchtend sein, dass wir mit unserer
fixen Aufteilung der Sudokurätsel in zwei Teile niemals mehr als zwei Kerne
beschäftigen können.
Wir benötigen daher eine flexiblere Strategie zur Aufteilung der Sudokurätsel
in parallele Berechnungen. Wir bedienen uns dabei eines Ansatzes der sich
dynamische Partitionierung nennt. Die Idee ist dass wir die Sudokurätsel
in viele kleine Einheiten aufteilen, und dass sich das Laufzeitsystem von Haskell
darum kümmert diese kleinen Einheiten in sinnvolle Arbeitspakete für einen Prozessorkern
zusammenzupacken. Mit diesem Ansatz lösen wir beide Probleme die mit unserer
ersten Version aufgetreten sind:
-
Es ist egal wie groß die einzelnen Teilprobleme sind. Wenn ein Prozessorkern
nichts mehr zu tun hat schiebt ihm das Laufzeitsystem neue Arbeit zu.
-
Wir müssen nicht im voraus die Anzahl der zur Verfügung stehenden Prozessorkerne
planen, denn das Laufzeitsystem kümmert sich auch um diesen Aspekt.
Hier nun die überarbeitete parallele Version mit dynamischer Partitionierung:
-- Datei SudokuPar2.hs
import Sudoku
import Driver
import Data.Maybe
import Control.Monad.Par
main = driver computeSolutions
where
computeSolutions puzzles =
filter isJust (runPar (parMap solve puzzles))
Der einzige Unterschied zur ursprünglichen, sequentiellen Version ist, dass wir anstelle von
map solve puzzles nun runPar (parMap solve puzzles) schreiben. Die Funktion
parMap kommt dabei aus dem Modul Control.Monad.Par. Der Aufruf
parMap solve puzzles ruft nun solve für jedes Rätsel in puzzles auf und
zwar so dass dem Laufzeitsystem Gelegenheit gegeben wird die Aufrufe von solve
geeignet zu parallelisieren. Sie sehen also: Parallelisierung ist in Haskell sehr einfach
und die monad-par Bibliothek garantiert, dass alles deterministisch abläuft
und dass keine Deadlocks oder sonstige, bei nebenläufigen Programmen typischen Probleme
auftreten.
Wir werden uns am Ende des Artikels auch noch die
Implementierung von parMap anschauen, wollen jetzt aber zunächst sehen welche
Performance unsere verbesserte parallele Version mit dynamischer Partitionierung
liefert:
Zunächst wieder eine sequentielle Ausführung als Lakmustest:
./SudokuPar2 +RTS -s -RTS sudoku17.1000.txt
Total time 1.51s ( 1.53s elapsed)
Und jetzt parallele Ausführungen mit zwei, drei und vier Kernen:
./SudokuPar2 +RTS -s -N2 -RTS sudoku17.1000.txt
Total time 1.54s ( 0.78s elapsed)
Speedup: 1,96
./SudokuPar2 +RTS -s -N3 -RTS sudoku17.1000.txt
Total time 1.55s ( 0.53s elapsed)
Speedup: 2,88
./SudokuPar2 +RTS -s -N4 -RTS sudoku17.1000.txt
Total time 1.56s ( 0.41s elapsed)
Speedup: 3,71
Ich habe testweise auch mal eine größere Eingabedatei mit 16.000 Sudokurätseln
getestet, hier ergeben sich sehr ähnliche Speedups.
Wie versprochen schauen wir uns zum Schluss noch eine mögliche
Implementierung von parMap an:
parMap f xs =
do bs <- mapM g xs
mapM get bs
where
g x =
do b <- new
fork (put b (f x))
return b
Die Funktion g legt für jedes Listenelement mit new eine neue Box and
und benutzt dann fork um f x parallel zu berechnen und das Ergebnis
in der Box zu speichern. Der Aufruf mapM g xs wendet nun g auf jedes Element
von xs an, so dass wir danach in bs die Boxen für die Ergebnisse von f
vorfinden. Schließlich holen wir mittels mapM get bs
die Ergebnisse aus den Boxen.
So, das war‘s für heute. Den Code zum Artikel finden Sie
hier.
Ich freue mich über jede Art von Rückmeldung!